


As computing systems increasingly involve concurrently acting autonomous agents, game-theoretic approaches are becoming widespread in computer science as a faithful modelling abstraction. These techniques can be used to reason about the competitive or collaborative behaviour of multiple rational agents or entities with distinct goals or objectives. We have developed a comprehensive set of techniques for verification and strategy synthesis for concurrent stochastic multi-agent games, covering finite and infinite horizon and a large class of probabilistic and reward objectives, as supported by the PRISM-games 3.0 software release.
Much of the work concerns zero-sum objectives, where a coalition of agents is aiming to maximise their expected reward, while the other agents aim to minimise this value. However, there are too limiting, as in many cases the agents will often have distinct, but not directly opposing goals, which cannot be modelled in a zero-sum fashion. We thus introduce equilibria, defined by a separate, independent objective for each agent. These are particularly attractive since they ensure stability against deviations by individual agents, improving the overall system outcomes. We consider Nash and correlated equilibria, and develop algorithms for their (approximate/exact) verification and synthesis for concurrent stochastic games. In a Nash equilibrium no agent has an incentive to deviate unilaterally from their strategy. Correlated equilibria, in which agents are able to coordinate through public signals, are easier to compute than Nash and can yield better outcomes.
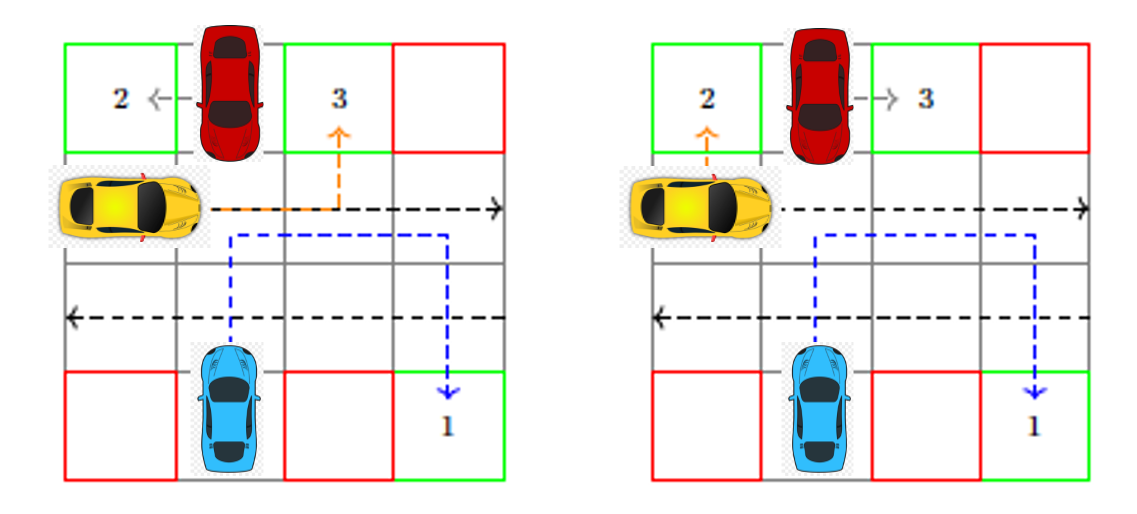
The image shows possible equilibria for a parking game. We consider a cost measure based on the distance each car needs to travel before parking, and if there is a crash. Although both strategies result in equilibria, given the cars are able to park without crashing, there is an advantage is selecting the one shown on the right, as the sum of distances travelled by all cars is smaller.
To select amongst the multiple equilibria, we consider two main types of optimality criteria, social welfare and social fairness. Social welfare maximises the sum of the agents’ rewards, whereas social cost minimises this value. On the other hand, social fairness, which minimises the differences between the objectives of individual players, is a novel optimality criterion inspired from economics that is distinct from the use of fairness in verification. Both optimality criteria can be employed for Nash and correlated equilibria.
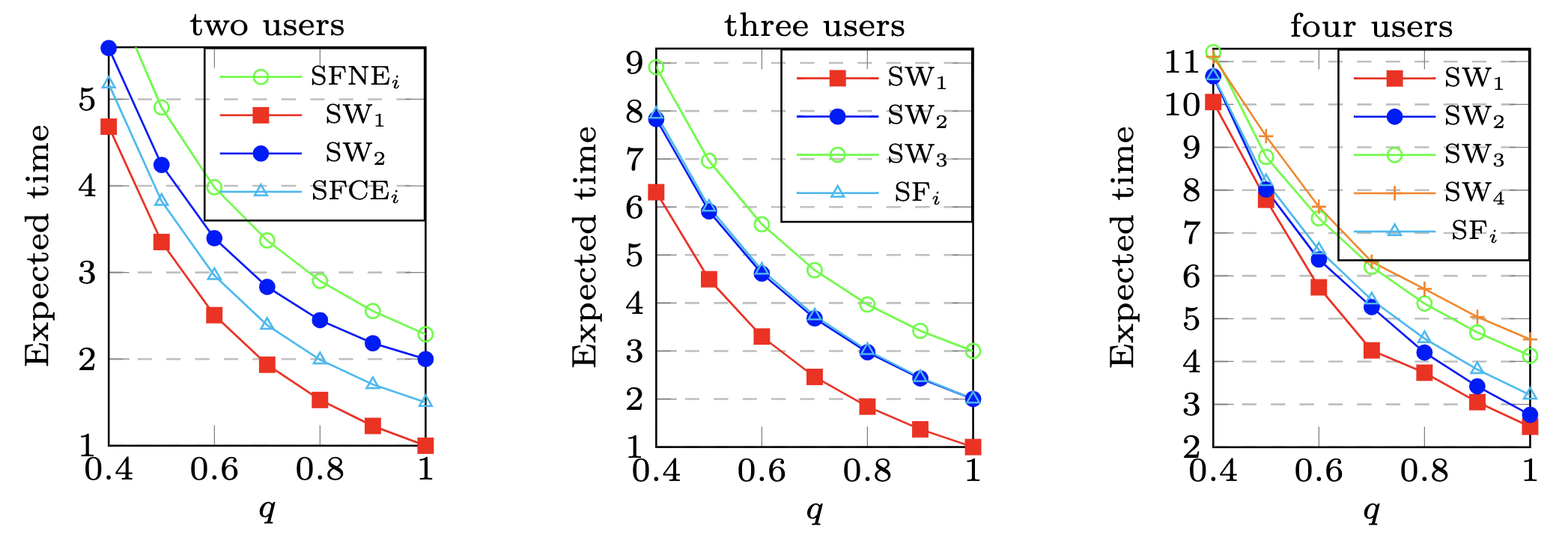
The image shows optimal values for agents trying to send packets using the slotted Aloha protocol. In this setting, if k users try to send a packet in the same time slot, the probability that each of them being successful is q/k, where q is a value between 0 and 1. If unsuccessful, an agent needs to wait a number of slots before resending set according to the Aloha’s exponential backoff scheme. In the figure, SWi correspond to the optimal values (expected times to send their packets) for agent i for both SWNE (social welfare Nash equilibria) and SWCE (social welfare correlated equilibria) for the cases of two, three and four users. We see that for these types of equilibria the values are different for each user, being lower for the agent that sends first and higher for that who sends last. On the other hand, for SFNE (social fair Nash equilibria) and SFCE (social fair correlated equilibria) the values for all agents coincide while for the latter the overall sum is only than 2% smaller when comparing to the social-welfare optimal variants.
Neuro-symbolic approaches to artificial intelligence, which combine neural networks with classical symbolic techniques, are growing in prominence, necessitating formal approaches to reason about their correctness. We have developed a novel modelling formalism called neuro-symbolic concurrent stochastic games (NS-CSGs), which comprise two probabilistic finite-state agents interacting in a shared continuous-state environment. Each agent observes the environment using a neural perception mechanism, which converts inputs such as images into symbolic percepts, and makes decisions symbolically. We focus on the class of NS-CSGs with Borel state spaces and prove the existence and measurability of the value function for zero-sum discounted cumulative rewards under piecewise-constant restrictions on the components of this class of models. To compute values and synthesise strategies, we developed practical value iteration (VI) and policy iteration (PI) algorithms to solve this new subclass of continuous-state CSGs by relying on a finite decomposition of the environment induced by the neural perception mechanisms, together with a finite representations of value functions and strategies.
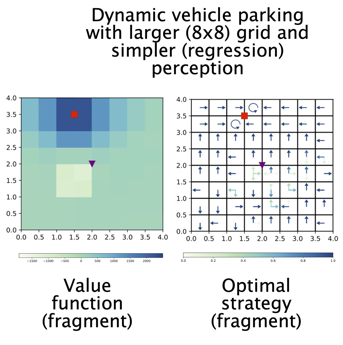
The image shows the value function and the computed strategy synthesised in the discounted, infinite-horizon setting for a dynamic car parking example modelled as a fully-observable zero-zum game.
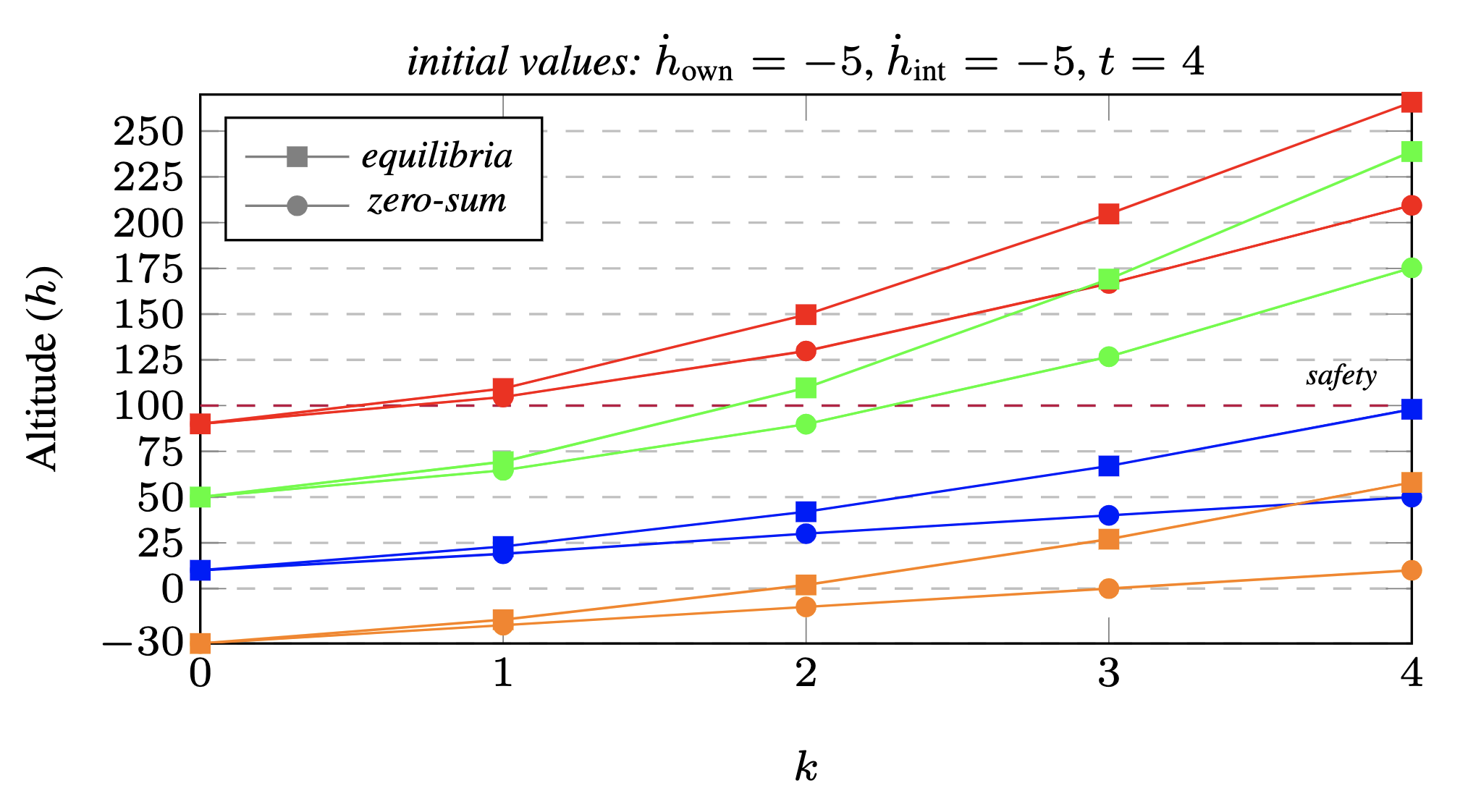
We considered (fully-observable) neuro-symbolic concurrent stochastic games with neural perception mechanisms, in which agents operate concurrently in a shared environment that they observe through neural networks. We have studied (undiscounted, finite-horizon) equilibria synthesis problem, which we have applied to the VCAS autonomous aircraft controller (also studied in the Robustness Guarantees for Bayesian Neural Networks theme) implemented as a ReLU network.
The figure plots the altitude h for equilibria and zero-sum strategies when maximising h for a given instant k. It can be seen that, with respect to the safety criterion of avoiding a near mid-air collision, equilibria strategies allow the two aircraft to reach a safe configuration within a shorter horizon, which would be missed by a zero-sum analysis.
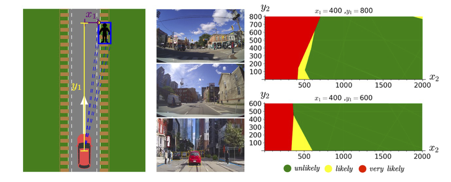
Stochastic games are an established model for multi-agent sequential decision making under uncertainty. In practical applications, though, agents often have only partial observability of their environment. Furthermore, agents increasingly perceive their environment using data-driven approaches such as neural networks trained on continuous data. We propose neuro-symbolic partially-observable stochastic games (NS-POSGs), a variant of continuous-space concurrent stochastic games that explicitly incorporates neural perception mechanisms. We focus on a one-sided setting with a partially-informed agent using discrete, data-driven observations and another, fully-informed agent. We present a new method, called one-sided NS-HSVI, for approximate solution of one-sided NS-POSGs, which exploits the piecewise constant structure of the model. Using neural network pre-image analysis to construct finite polyhedral representations and particle-based representations for beliefs, we implement our approach and illustrate its practical applicability to the analysis of pedestrian-vehicle and pursuit-evasion scenarios.
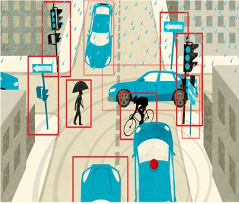
The image shows a pedestrian-vehicle example to analyse decision making for an autonomous vehicle using an intention estimation model for a pedestrian at a crossing. The scenario is modelled as a one-sided game, where the first, partially-informed agent represents the vehicle. It observes the environment (comprising the successive pedestrian locations) using a neural network perception mechanism to predict the pedestrian’s intention. The perception function takes two successive (relative) locations of the pedestrian (the top-left coordinates (x1, y1) and (x2, y2) of two fixed size bounding boxes around the pedestrian) and classifies its intention as: unlikely, likely or very likely to cross. We train a feed-forward neural network classifier with ReLU activation functions over the PIE dataset. The second agent, the pedestrian, is fully informed, providing a worst-case analysis of the vehicle decisions, and can decide to cross or return to the roadside. The goal of the vehicle is to minimise the likelihood of a collision with the pedestrian, which is achieved by associating a negative reward with this event.
Left: Positions of two agents. Middle: Sample images from the PIE dataset. Right: Slices of learnt perception function, where (x1,y1), (x2,y2) are two successive (relative) positions of the pedestrian.
To know more about these models and analysis techniques, follow the links below.