Robustness to causal interventions. Distribution shifts.

Robustness of decision rules to shifts in the data-generating process is crucial to the successful deployment of decision-making systems, since they have to be applied to input points outside of the data distribution they were trained on. Local adversarial robustness guarantees that the prediction does not change in some vicinity of a specific input point, whereas we are instead interested in distribution shifts. Such shifts can be viewed as interventions on a causal graph, which capture (possibly hypothetical) changes in the data-generating process, whether due to natural reasons or by the action of an adversary.

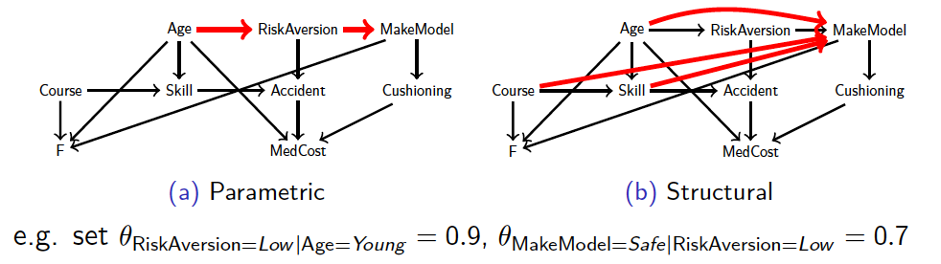
The diagram shows a causal Bayesian network of an insurance model under two types of such shifts, parametric (change of conditional probability values) and structural (removal/addition of causal links).

Interventional robustness via arithmetic circuits. Provable guarantees.

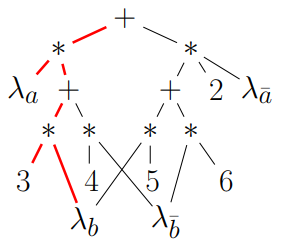
We formally define the interventional robustness problem, a novel model-based notion of robustness for decision functions that measures worst-case performance with respect to a set of interventions that denote changes to parameters and/or causal influences. While the problem itself is exponential, by relying on a tractable representation of Bayesian networks as arithmetic circuits, also in the presence of data uncertainty, we provide efficient algorithms for computing guaranteed upper and lower bounds on the interventional robustness probabilities. To this end, we exploit the efficient compilation of Bayesian networks into arithmetic circuits (see image), and compile the decision function and the data-generating process jointly.

Tractable structure learning via product-sum networks.

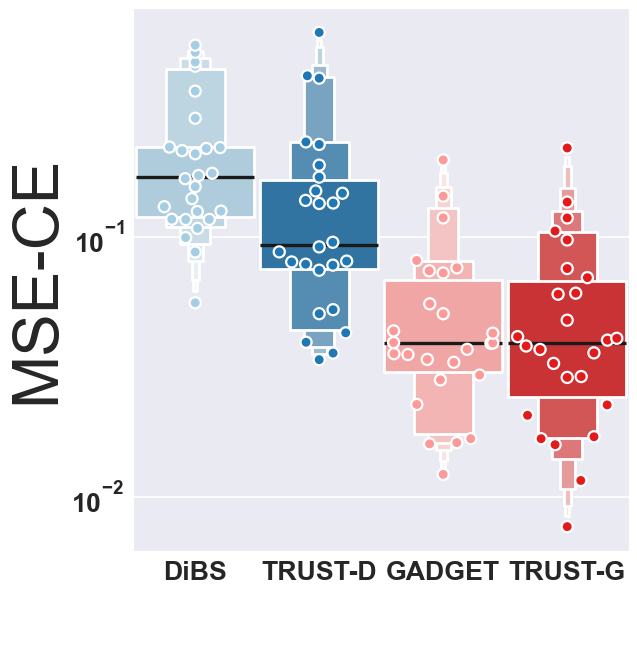
Bayesian structure learning allows one to capture uncertainty over the causal directed acyclic graph (DAG) responsible for generating given data. We develop a TRUST (Tractable Uncertainty for STructure learning) framework, which supports approximate posterior inference that relies on probabilistic circuits as the representation of posterior belief. In contrast to sample-based posterior approximations, our representation can capture a much richer space of DAGs, while being able to tractably answer a range of useful inference queries. We empirically show how probabilistic circuits can be used as an augmented representation for structure learning methods, leading to improvement in both the quality of inferred structures and posterior uncertainty, and show how causality queries can be estimated.

The image shows MSE (Mean Squared Error) of Causal Effects (lower is better) for TRUST in comparison with state of the art.

Learning decision policies by leveraging causal inference. Suboptimality guarantees.

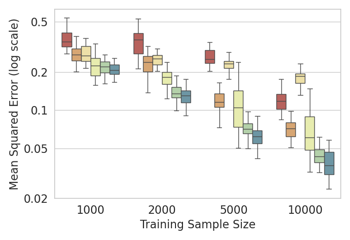
A common issue in learning decision-making policies in data-rich settings is spurious correlations in the offline dataset, which can be caused by hidden confounders. We exploit causal inference in the context of instrumental variable (IV) regression to learn causal relationships between confounded action, outcome, and context variables. Most recent IV regression algorithms use a two-stage approach, where a deep neural network (DNN) estimator learnt in the first stage is directly plugged into the second stage, in which another DNN is used to estimate the causal effect. Naively plugging the estimator can cause heavy bias in the second stage, especially when regularisation bias is present in the first stage estimator. We propose DML-IV, a non-linear IV regression method that leverages double/debiased machine learning (DML) framework to reduce the bias in two-stage IV regressions and effectively learns high-performing policies. The learnt DML-IV estimator has strong convergence rate and suboptimality guarantees that match those when the dataset is unconfounded.

The plot shows mean square error (MSE) for our method (green and turquoise) compared to state of the art.

Imitation learning with hidden confounders. Upper bounding the imitation gap.

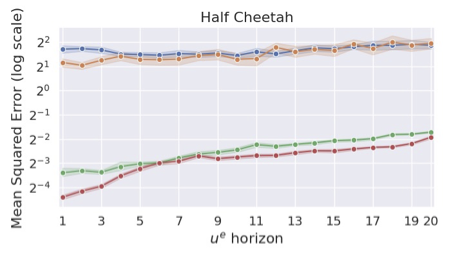
Imitation Learning (IL) has emerged as a prominent paradigm in machine learning, where the objective is to learn a policy that mimics the behaviour of an expert by learning from its demonstrations. We propose a general and unifying framework for causal Imitation Learning (IL) with hidden confounders, which subsumes several existing settings. Our framework accounts for two types of hidden confounders: (a) variables observed by the expert but not by the imitator, and (b) confounding noise hidden from both. By leveraging trajectory histories as instruments, we reformulate causal IL in our framework into a Conditional Moment Restriction (CMR) problem. We propose DML-IL, an algorithm that solves these CMRs via instrumental variable regression, and upper bound its imitation gap. Empirical evaluation on continuous state-action environments, including Mujoco tasks, shows that DML-IL outperforms existing causal IL baselines.

The plot shows mean squared error (MSE) for our method (red) compared to state of the art on the Half-Cheetah environment in Mujoco.